Our new, cake-themed paper on nanostructured permanent magnets has now been published in Applied Physics Letters.
In the paper we present results from micromagnetic simulations that assess the performance of multi-phase nanostructured permanent magnets, whose cross-section resemble that of a Battenberg cake. By including a super-hard outer shell we are able to counteract the effects of thermal fluctuations and surface defects, both of which are detrimental to the performance of such permanent magnets. Such magnets are important for the motors in electric vehicles and for the generators in wind turbines, and these machines usually operate at elevated temperatures.
Click here to download the author-formatted reprint (free) or here for the official, journal-formatted version ($).
Figure: A home made Battenberg Cake, end view, with a slice leaning on it [Creative Commons Attribution 3.0 Unported – Author:Henrycooksey, Wikimedia Commons]
In case you are wondering, the soft cores in our magnet are like the sponge, the interdiffusion layer is like the jam-sponge mix you get at the surfaces of the sponge, the hard matrix is the jam and the super hard shell is like the marzipan. The difference is that our model has 3D periodicity while a typical Battenberg cake has only 2D periodicity, like a checkerboard prism.
Battenberg cakes can be made in a number of different configurations, and so can Battenberg magnets! Stay tuned for more cake-inspired magnetic nanostructures in the future!
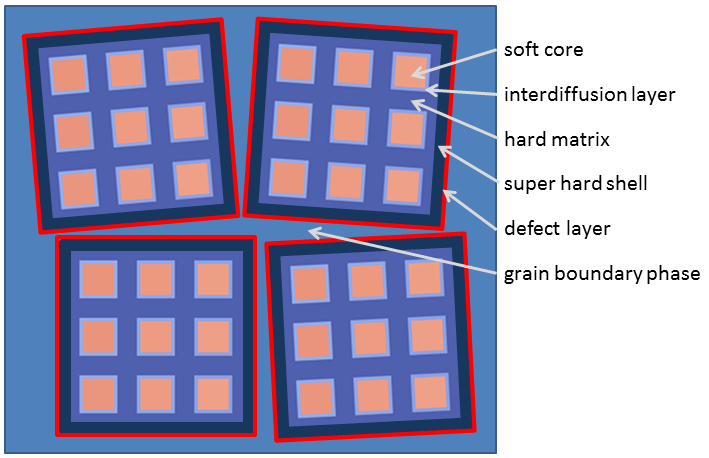Fig. 1 Proposed microstructure of a nano-composite per-manent magnet. Each grain is composed of soft magneticinclusions embedded in a hard magnetic phase. Both phasesare coupled through a thin inter-diffusion layer with proper-ties that may be different from either of the two phases. Agrain may have a super-hard shell with an anisotropy fieldexceeding that of the hard magnetic matrix phase. At thesurface a ferromagnetic layer with small or zero anisotropy isassumed (defect layer).
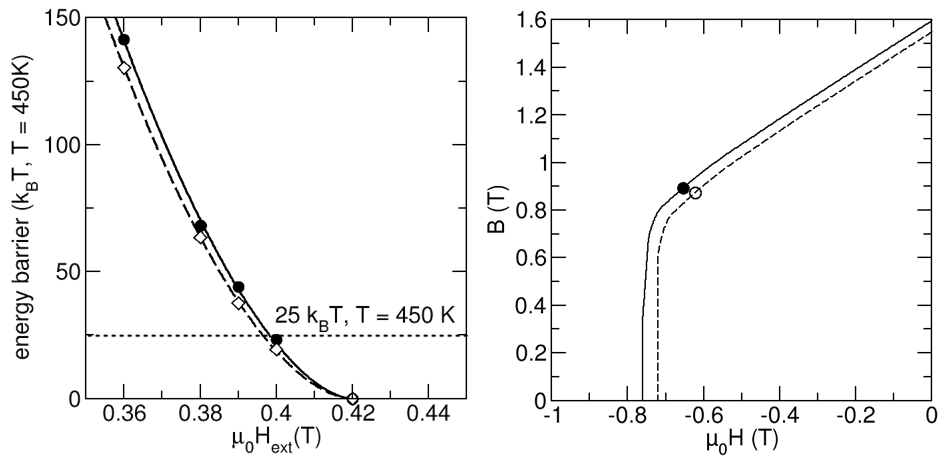Fig. 2 Left: Data and fit of the energy barrier ofa single grain as function of the applied field withoutthe super-hard shell (hollow diamonds and dashed line)and with (filled circles and solid line). Right: B(H)loops for a single grain at 450 K. The circles indicatethe working point where the energy product reaches itsmaximum. Dashed lines: Fe 65 Co 35 /Nd 2 Fe 14 B, solid lines:Fe 65 Co 35 /Nd 2 Fe 14 B/Sm 2 Fe 17 N 3 .